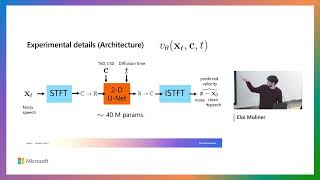
Microsoft Research335 тыс
Популярные
Опубликовано 12 июля 2016, 18:17
Fix a prime power $q$. A triangle in $\mathbb{F}_q^n$ is a triple $x,y,z$ of elements with $x+y=z$. Green's triangle removal lemma in $\mathbb{F}_q^n$ states that for each $\epsilon>0$ there is a $\delta>0$ such that every subset of $\mathbb{F}_q^n$ which has few triangles (less than $\delta N^2$, where $N=q^n$ is the total number of elements), can be made triangle-free by removing few elements (less than $\epsilon N$). Previously, the best known bound was of tower type. Using a result of Kleinberg-Speyer, which builds on the breakthrough work of Croot-Lev-Pach on the cap set problem, and subsequent work by Ellenberg-Gijswijt and Blasiak-Church-Cohn-Grochow-Umans, we prove a polynomial bound for Green's triangle removal lemma, which we can prove is tight for small q, and conjecture it is tight for all q. Joint work with Jacob Fox.
Свежие видео